fabulousuf.blogg.se - Sap 2000 beam to beam connection

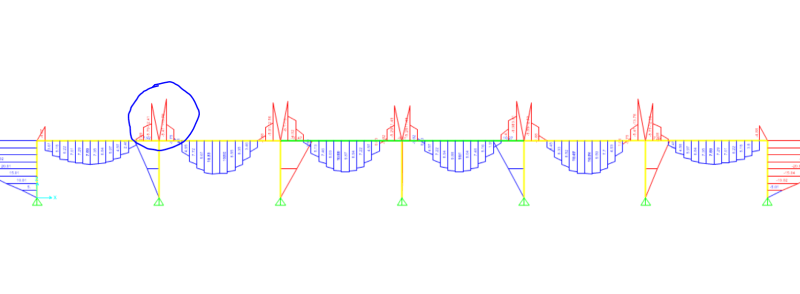
Therefore, M x = 90 kNm < M b / m LT = 239.838 kNm Λ LO < λ LT Therefore check for lateral torsional bucklingįrom Table 16, for λ LT = 114.6 P b = 102 N/mm 2

If λ LO ≥ λ LT no allowance needs to be made for lateral-torsional buckling and otherwise check for lateral-torsional buckling.

If λ LO ≥ λ LT P b = P y or Othewise P b shall be taken from Table 16 for rolled sections. Λ LO can be obtained from Table 16 (refer bottom of the table) V – slenderness factor to be obtained from Table 19 based on the λ / x and η Β w = 1 for Class 1 plastic or Class 2 Compact sections L E – to be taken from Table 13 as per the Cl. In this steel beam design example, we discussed both the methods to elaborate on the procedures that need to be followed using either method.įurther, the main difference between these two methods is evaluating bending strength. They are the rigorous method and the simplified method. There are two methods to check lateral-torsional buckling as discussed in the article steel beam design as per BS 5950. In this example, no intermediate restrains were considered The first step of the steel beam design is the classification of the section to know whether it is plastic, semi-plastic, compact, slender.īending ok Check Lateral Torsional Buckling Under this steel beam design calculation, the following checks are done. Let’s start the steel beam design calculation.

Desing strength of steel, Py = 275 N/mm 2Ĭonsider universal beam 500x200x89.7 kg/m (P y = 275 N/mm 2 ) Section Data.

Theoretical aspects and code design procedures are discussed in the article design of the steel beam as per BS 5950. The beam is considered as simply supported and the design data for calculating the bending moment and shear forces are given below.įurther, the section properties to be considered are also given in each stage fo checking the section.

The steel beam design worked example elaborates the design of a simply supported beam having a uniformly distributed load.